fungal music - jacques & fran soddell
WHAT ARE L-SYSTEMS?
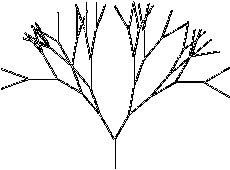
In 1968 Aristid Lindenmayer, a biologist who worked with yeast and filamentous fungi, published a description of L-systems (Lindenmayer systems). These were string rewriting systems that could be used to describe the growth of a filamentous cyanobacterium (blue-green alga) called Anabaena. Rewriting is a technique for defining complex objects by successively replacing parts of a simple initial string using a set of rewriting rules or productions. (Prusinkiewicz & Lindenmayer, 1990). However, the application of L-systems took a large leap when the strings generated by the production rules were interpreted using turtle graphics by Smith (1984), so that a simple axiom and production rules could code for a relatively complex plant. This was further developed by Prusinkiewicz, Hanan and Lindenmayer in their extensive work with modelling plants and trees. These simple string rewriting systems were Deterministic L systems -
Turtle Graphics
The most common interpretation of L-systems is a graphical one using Turtle graphics, where pen movements are represented by symbols such as F (pen down, move forward one step), f (pen up, move forward one step), + (turn left by predefined angle), - (turn right by predefined angle).
Generations
At each generation, when the string is rewritten, the string gets longer and the resulting image (tree, microbe, fractal etc) is more complex.
Stochastic and Parametric L-systems
A number of variations to L-systems have been introduced, including Stochastic L-systems, where irregularity is introduced by giving probabilities to the production rules. Another important improvement was the introduction of Parametric L-systems, which include the ability to pass parameters. Examples of these are presented below.. Other types of L-systems have also been described.
Uses of L-system
L-systems have been extensively used to model plant growth and are used in computer graphics to generate complex images from simple rules eg fractal objects.
References
Prusinkiewicz P & Hanan (1989) Lindenmayer systems, plants and fractals. Lecture Notes in Biomathematics. Springer-Verlag: Berlin.
Prusinkiewicz P & Lindenmayer A (1990). The Algorithmic Beauty of Plants. Springer-Verlag: Berlin.
Smith A (1984) Plants, fractals and formal languages. Computer Graphics 18 (July) 1-10
Some L-systems Links
An Introduction to Lindenmayer Systems by Gabriela Ochoa
L systems Software
Using Lindenmayer Systems to Investigate How Filamentous Fungi May Produce Round Colonies by Fran Soddell, Robert Seviour & Jacques Soddell